3550. Smallest Index With Digit Sum Equal to Index#
题目#
3550. Smallest Index With Digit Sum Equal to Index
给定一个整数数组 nums,返回满足 nums[i] 的各位数字之和等于索引 i 条件的最小索引 i;如果不存在,那么返回 -1
这个题的约束是
1 <= nums.length <= 1000 <= nums[i] <= 1000
思路#
- 数值是整数,并且本身在
1000之内,看起来不需要额外考虑 - 数组长度最大只有
100并且非空
直接顺序遍历判断即可
package main
import (
"fmt"
)
func sumOfDigits(num int) int {
sum := 0
for num > 0 {
sum += num % 10
num /= 10
}
return sum
}
func smallestIndex(nums []int) int {
for i, num := range nums {
if sumOfDigits(num) == i {
return i
}
}
return -1
}
func main() {
fmt.Println(smallestIndex([]int{1, 3, 2})) // 2
fmt.Println(smallestIndex([]int{1, 10, 11})) // 1
fmt.Println(smallestIndex([]int{1, 2, 3})) // -1
}
3551. Minimum Swaps to Sort by Digit Sum#
题目#
3551. Minimum Swaps to Sort by Digit Sum
给定一个由 互不相同的正整数 组成的数组 nums。需要根据每个数字的数位和来升序排列数组:
- 如果两个数字的数位和相同,则数值较小的数字排在前面。
返回:将数组 nums 排成这种排序顺序所需的最小交换次数。
示例:
输入:nums = [18, 43, 34, 16]
- 数位和:[9, 7, 7, 7]
- 按规则排序后:[16, 34, 43, 18]
- 所以:
18↔16:1 次43↔34:1 次 → 共需要 2 次交换 输出:2
思路#
- 可以复用上一道题的
sumOfDigits函数 - 求解数组排序元素间所需最小交换次数这类问题可以使用置换环, 可以参考 https://www.cnblogs.com/TTS-TTS/p/17047104.html。排序所需最小交换次数为
数组长度-环的个数
package main
import (
"fmt"
"sort"
)
func sumOfDigits(num int) int {
sum := 0
for num > 0 {
sum += num % 10
num /= 10
}
return sum
}
func minSwaps(nums []int) int {
numsLen := len(nums)
type Pair struct {
value int
index int // original index
digitSum int // sum of digits
}
original := make([]Pair, numsLen)
for i := 0; i < numsLen; i++ {
original[i] = Pair{
value: nums[i],
index: i,
digitSum: sumOfDigits(nums[i]),
}
}
sorted := make([]Pair, numsLen)
copy(sorted, original)
// 排序目标数组:按 digit sum 升序,若相等按值升序
sort.Slice(sorted, func(i, j int) bool {
if sorted[i].digitSum < sorted[j].digitSum {
return true
} else if sorted[i].digitSum > sorted[j].digitSum {
return false
} else {
return sorted[i].value < sorted[j].value
}
})
// 构建原 index 到目标 index 的映射
pos := make([]int, numsLen) // pos[i] 表示原始位置 i 的元素要去的位置
isAllSame := true // fast path 如果排序前后下标均相同,那么直接返回 0
for i := 0; i < numsLen; i++ {
pos[sorted[i].index] = i
if isAllSame && sorted[i].index != i {
isAllSame = false
}
}
if isAllSame {
return 0
}
// 计算最小交换次数(利用置换环)
visited := make([]bool, numsLen)
swaps := 0
for i := 0; i < numsLen; i++ {
if visited[i] || pos[i] == i {
continue
}
// 找一个环
cycleLen := 0
j := i
for !visited[j] {
visited[j] = true
j = pos[j]
cycleLen++
}
if cycleLen > 0 {
swaps += cycleLen - 1
}
}
return swaps
}
func main() {
fmt.Println(minSwaps([]int{37, 100})) // 1
fmt.Println(minSwaps([]int{22, 14, 33, 7})) // 0
fmt.Println(minSwaps([]int{18, 43, 34, 16})) // 2
}
3552. Grid Teleportation Traversal#
题目#
3552. Grid Teleportation Traversal
给你一个大小为 m x n 的二维字符网格 matrix,用字符串数组表示,其中 matrix[i][j] 表示第 i 行和第 j 列处的单元格。每个单元格可以是以下几种字符之一:
'.'表示一个空单元格。'#'表示一个障碍物。- 一个大写字母(
'A'到'Z')表示一个传送门。
你从左上角单元格 (0, 0) 出发,目标是到达右下角单元格 (m - 1, n - 1)。你可以从当前位置移动到相邻的单元格(上、下、左、右),移动后的单元格必须在网格边界内且不是障碍物**。**
如果你踏入一个包含传送门字母的单元格,并且你之前没有使用过该传送门字母,你可以立即传送到网格中另一个具有相同字母的单元格。这次传送不计入移动次数,但每个字母对应的传送门在旅程中 最多 只能使用一次。
返回到达右下角单元格所需的 最少 移动次数。如果无法到达目的地,则返回 -1。
示例 1:
输入: matrix = [“A..”,".A.","…"]
输出: 2
解释:
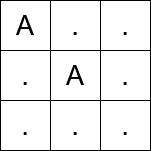
- 在第一次移动之前,从
(0, 0)传送到(1, 1)。 - 第一次移动,从
(1, 1)移动到(1, 2)。 - 第二次移动,从
(1, 2)移动到(2, 2)。
思路#
我们可以把这个矩阵看作一个无权图
每个格子是一个节点。
从一个可通行的格子可以走向上下左右四个方向。
如果当前格子是传送门,还可以“瞬移”到所有同样字母的格子。
这些“移动”或“传送”操作的 cost 都是 1
通过 BFS 的思路,按照层次遍历。从左上角出发首先探索距离起点为 1 的所有节点;然后是距离为 2 的节点;然后是 3,4,5…
当我们第一次碰到右下角的时候,便是最短的路径
package main
import (
"container/list"
"fmt"
)
type Position struct {
row int
col int
}
func isPortal(ch byte) bool {
return ch >= 'A' && ch <= 'Z'
}
func isObstacle(ch byte) bool {
return ch == '#'
}
func isEmptyCell(ch byte) bool {
return ch == '.'
}
func minMoves(matrix []string) int {
rows, cols := len(matrix), len(matrix[0])
grid := make([][]byte, rows)
for i := range matrix {
grid[i] = []byte(matrix[i])
}
portals := make(map[byte][]Position)
// 取出所有的传送门
for r := 0; r < rows; r++ {
for c := 0; c < cols; c++ {
ch := grid[r][c]
if isPortal(ch) {
portals[ch] = append(portals[ch], Position{r, c})
}
}
}
usedPortals := make(map[byte]bool)
queue := list.New()
start := grid[0][0]
// 处理起始位置,初始化 BFS
if isObstacle(start) {
return -1
} else if isEmptyCell(start) {
queue.PushBack(Position{0, 0})
grid[0][0] = '#'
} else if isPortal(start) {
for _, p := range portals[start] {
queue.PushBack(p)
grid[p.row][p.col] = '#'
}
usedPortals[start] = true
} else {
panic("Invalid chars")
}
steps := 0
// BFS
for queue.Len() > 0 {
for i := queue.Len(); i > 0; i-- {
curr := queue.Remove(queue.Front()).(Position)
if curr.row == rows-1 && curr.col == cols-1 {
return steps
}
// 尝试四方向移动
for _, d := range [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}} {
nextRow, newCol := curr.row+d[0], curr.col+d[1]
// 越界?
if nextRow >= 0 && nextRow < rows && newCol >= 0 && newCol < cols {
ch := grid[nextRow][newCol]
switch {
case isEmptyCell(ch):
queue.PushBack(Position{nextRow, newCol})
grid[nextRow][newCol] = '#'
case isPortal(ch) && !usedPortals[ch]:
for _, p := range portals[ch] {
queue.PushBack(p)
grid[p.row][p.col] = '#'
}
usedPortals[ch] = true
}
}
}
}
steps++
}
return -1
}
func main() {
fmt.Println(minMoves([]string{"A..", ".A.", "..."})) // Output: 2
fmt.Println(minMoves([]string{".#...", ".#.#.", ".#.#.", "...#."})) // Output: 13
fmt.Println(minMoves([]string{".A", "CA"})) // Output: 1
}
3553. Minimum Weighted Subgraph With the Required Paths II#
题目#
3553. Minimum Weighted Subgraph With the Required Paths II
树有 n 个节点,编号 0 ~ n-1,edges[i] = [u, v, w] 表示 u 和 v 之间有条权重为 w 的边。queries[j] = [src1, src2, dest],要求找到一个包含 src1, src2, dest 的连通子树,且在该子树中 src1 和 src2 都可以走到 dest。求这个子树的最小权重和
比如这个例子
Input: edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], queries = [[2,3,4],[0,2,5]]

需要输出
answer[0]: The total weight of the selected subtree that ensures a path fromsrc1 = 2andsrc2 = 3todest = 4is3 + 5 + 4 = 12.answer[1]: The total weight of the selected subtree that ensures a path fromsrc1 = 0andsrc2 = 2todest = 5is2 + 3 + 6 = 11.
思路#
树是无环的
src1、src2、dest三点不同
在树中,两个节点之间的路径是唯一的。
我们设:
dist[x]表示节点 x 到根的路径总权重。lca(u, v)表示节点 u 和 v 的最近公共祖先。
有以下公式:
\(dist(u,v)=dist[u]+dist[v]−2⋅dist[lca(u,v)]\)
如果我们想要计算三点的最小子树权重,它等于:
\(dist[A]+dist[B]+dist[C]−dist[lca(A,B)]−dist[lca(B,C)]−dist[lca(C,A)]\)
这里参考倍增法求解 LCA https://www.cnblogs.com/ofnoname/p/18823468
package main
import (
"fmt"
)
type Edge struct {
dest int
weight int
}
var (
LOG int
tree [][]Edge // 邻接表
depth []int // 每个节点的深度
dist []int // 每个节点到根的距离
// parent[u][k] 表示:从节点 u 往上跳 2^k 步后的祖先节点。
// 举例来说:
// parent[u][0] 是 u 的直接父亲。
// parent[u][1] 是 u 的祖父(跳两步)。
// parent[u][2] 是 u 的曾祖父(跳四步)。
parent [][]int
)
func dfs(u, p, d, w int) {
depth[u] = d
parent[u][0] = p
dist[u] = w
for _, e := range tree[u] {
if e.dest != p {
dfs(e.dest, u, d+1, w+e.weight)
}
}
}
func initLCA(n int) {
for k := 1; k < LOG; k++ {
for u := 0; u < n; u++ {
if parent[u][k-1] != -1 {
parent[u][k] = parent[parent[u][k-1]][k-1]
} else {
parent[u][k] = -1
}
}
}
}
func lca(u, v int) int {
if depth[u] < depth[v] {
u, v = v, u
}
// 把u提升到和v同一深度
for i := LOG - 1; i >= 0; i-- {
if parent[u][i] != -1 && depth[parent[u][i]] >= depth[v] {
u = parent[u][i]
}
}
if u == v {
return u
}
// 同步提升u,v
for i := LOG - 1; i >= 0; i-- {
if parent[u][i] != -1 && parent[u][i] != parent[v][i] {
u = parent[u][i]
v = parent[v][i]
}
}
return parent[u][0]
}
func minimumWeight(edges [][]int, queries [][]int) []int {
n := len(edges) + 1
LOG = 1 // 倍增法中需要的最大层数
for (1 << LOG) <= n {
LOG++
}
tree = make([][]Edge, n)
for _, e := range edges {
src, dest, weight := e[0], e[1], e[2]
// 无向树
tree[src] = append(tree[src], Edge{dest, weight})
tree[dest] = append(tree[dest], Edge{src, weight})
}
depth = make([]int, n)
dist = make([]int, n)
parent = make([][]int, n)
for i := range parent {
parent[i] = make([]int, LOG)
for j := range parent[i] {
parent[i][j] = -1
}
}
dfs(0, -1, 0, 0)
initLCA(n)
result := make([]int, len(queries))
for i, q := range queries {
src1, src2, dest := q[0], q[1], q[2]
lca1 := lca(src1, src2)
lca2 := lca(src2, dest)
lca3 := lca(dest, src1)
// 三点子树权重和
result[i] = dist[src1] + dist[src2] + dist[dest] - dist[lca1] - dist[lca2] - dist[lca3]
}
return result
}
func main() {
edges := [][]int{{0, 1, 2}, {1, 2, 3}, {1, 3, 5}, {1, 4, 4}, {2, 5, 6}}
queries := [][]int{{2, 3, 4}, {0, 2, 5}}
fmt.Println(minimumWeight(edges, queries)) // [12 11]
edges2 := [][]int{{1, 0, 8}, {0, 2, 7}}
queries2 := [][]int{{0, 1, 2}}
fmt.Println(minimumWeight(edges2, queries2)) // [15]
}
置换环#
对于输入数组 A
[a1, a2, a3, a4, a5, a6]
经过若干次元素交换,可以得到数组 B
[b1, b2, b3, b4, b5, b6]
对于每个元素 A[i],和其在 B 中对应的元素 B[j],我们可以构建一个映射关系 i -> j,记作 f(i)。我们进行分类讨论
i = j,即经过 N 次交换后元素的位置不变。此时我们的最小交换次数可以不考虑这个元素(相当于没有交换此元素)i != j,我们经过交换后,使用原数组i位置的元素替换了原数组j位置的元素。那么原数组j位置的元素,我们也可以通过映射关系f来得到新的位置k。此时有两种情况i = k,我们实现了两个元素的交换,最小交换次数为 1i != k,我们可以递归此过程,计算f(k)的值,依次类推下去…我们会重复遍历到(i, j, k ...)中的一个位置,产生一个环
用实际例子来看一下:
假设输入数组 A 为
[1, 2, 3]
- 如果
f(0) = 1,f(1) = 0,我们会得到
[2, 1, 3]
- 如果
f(0) = 1,f(1) = 2,f(2) = 0,我们会得到
[3, 1, 2]
首先对于一个长度为 k 的环,我们通过交换得到目标排列的的最小交换次数是 k - 1。这个可以由数学归纳法证明
对于 k = 1
- 环:仅有一个元素
a1,它已经在正确的位置 - 交换次数:1 - 1 = 0 次(无需交换)
对于 k > 1
已知在不改变环长度的条件下,继续任意交换元素,并不影响最小交换次数。比如 [1, 2, 3] 交换为 [3, 1, 2] 和 [2, 3, 1] 的最小次数是一样的。不妨考虑一个长度为 k 的循环右移的环:a1→a2→⋯→ak→a1。
- 第一步交换:交换
a1和a2的位置。a1归位到正确位置,a2被移动到原a的位置。- 剩余元素形成一个长度为
k - 1的环a2→a3→⋯→ak→a2。
- 应用归纳假设:剩余长度为
k−1的环需要(k−1)−1=k−2次交换。
每次交换至少归位一个元素,并将剩余部分分解为更小的环。依次类推得到 k - 1
有了这个结论,我们可以计算长度为 n 的数组。将其划分为 m 个环。每个环的长度是 k1, k2, k3, ... km。所以总共的最小交换次数是 (k1 - 1) + (k2 - 1) + ... +(km -1) ,计算后得到 (k1 + k2 + k3 ... +km) - m ,得到 n - m
举例
A = [0, 1, 2, 3, 4, 5]
B = [0, 3, 1, 4, 2, 5]
映射关系
0 -> 0 自环,长度 1
1 -> 2 -> 4 -> 3 -> 1 长度 4
5 -> 5 自环, 长度 1
所以最小交换的次数为元素个数 6 减去 环的个数 3 ,为 3
模版代码如下
package main
func minSwaps(source, target []int) int {
n := len(source)
if n != len(target) {
panic("")
}
posInSource := make(map[int]int, n)
for i, val := range source {
posInSource[val] = i
}
pos := make([]int, n)
for i := 0; i < n; i++ {
pos[i] = posInSource[target[i]]
}
visited := make([]bool, n)
swaps := 0
for i := 0; i < n; i++ {
if visited[i] || pos[i] == i {
continue
}
cycleLen := 0
j := i
for !visited[j] {
visited[j] = true
j = pos[j]
cycleLen++
}
swaps += cycleLen - 1
}
return swaps
}
func main() {
a := []int{0, 1, 2}
// a := []int{1, 0, 2}
// a := []int{2, 0, 1}
b := []int{2, 0, 1}
println(minSwaps(a, b)) // Output: 2
a = []int{3, 5, 4, 1, 2, 0}
// a = []int{1, 5, 4, 3, 2, 0}
// a = []int{5, 1, 4, 3, 2, 0}
// a = []int{0, 1, 4, 3, 2, 5}
// a = []int{0, 1, 2, 3, 4, 5}
b = []int{0, 1, 2, 3, 4, 5}
println(minSwaps(a, b)) // Output: 4
a = []int{0}
b = []int{0}
println(minSwaps(a, b)) // Output: 0
}